Without intervals Western music would not exist as it does today. So understanding them is crucial to developing you understanding of music theory. In the article, we’ll give you a rock solid foundation in the main three types: major intervals, minor intervals and perfect intervals.
What is an interval?
An interval is defined as the distance between two notes. We could play the notes at the same time, a harmonic interval, or one after another, creating a melodic interval.

Naming intervals
But how can we describe the distance between two notes? Well the simplest way would be to say how many half-steps or whole steps are between the 2 notes.
Take the interval C natural – E natural. Looking on the piano you can easily see that these notes are 4 half-steps (semitones) apart OR 2 whole steps (tones).
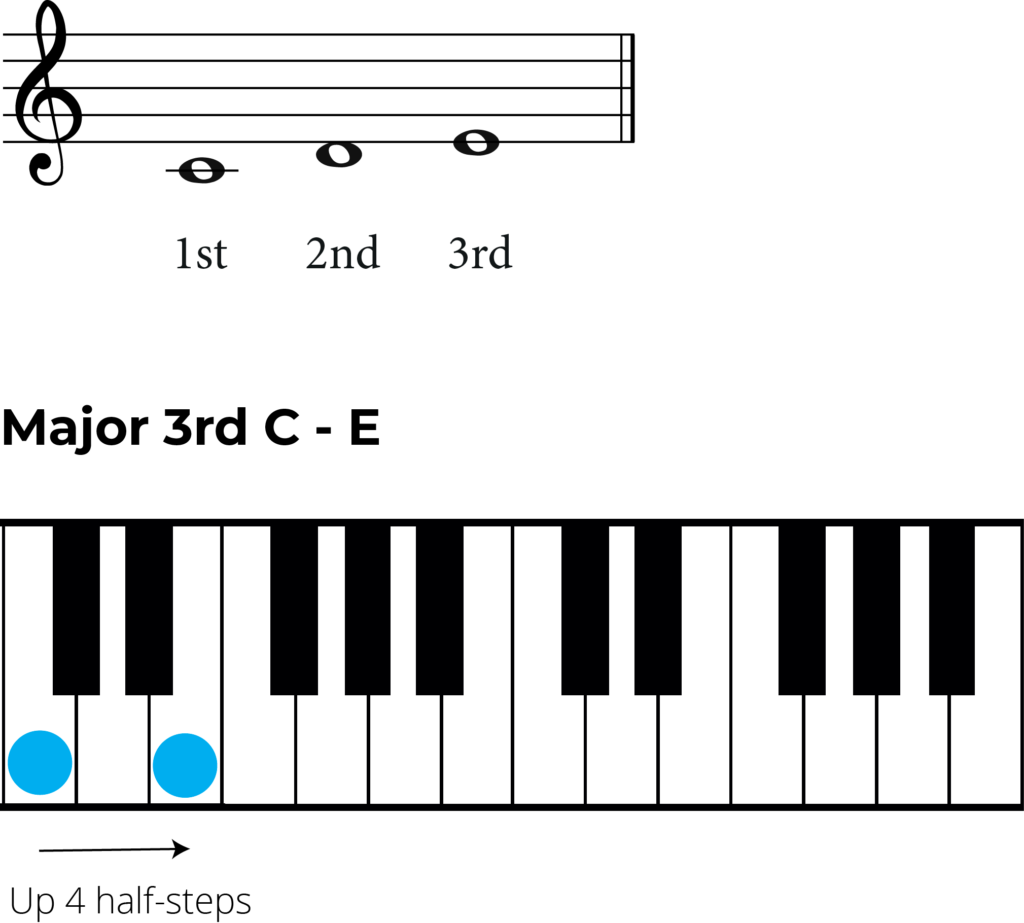
But wait, this isn’t going to help me with major, minor and perfect! What do all those mean? Well, you’d be right. The other ways to label intervals are according to their quality. And for this we need to think about scales.
Let’s look at an example.
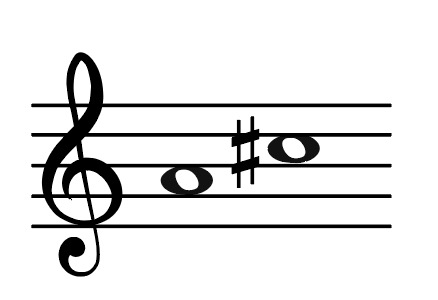
Now this interval is a 3rd. We know it’s a 3rd because it C is the 3rd degree of the A major scale.

We can work out the number of the interval simply by ignoring any accidentals and asking ourselves, ‘What degree of the scale is the top note?’ In this example we have A….B…C so the 3rd degree. A – G would be a 7th, A – B a 2nd… and so on.
But what type of interval is it: major, minor or perfect? It is actually a Major interval, a Major 3rd to be exact.
If a note is in the major scale of the lower note (and is a 2nd, 3rd, 6th or 7th) then it is a major interval.
Major Intervals, Minor Intervals, Perfect intervals
Here is a handy table used to so that you know which intervals can be major/minor and which are perfect intervals.

Major intervals and Minor Intervals
Let’s look at an example of a major interval and how to name it.

What is the number of this interval?
That’s correct, it is a second! Now ask yourself, is D natural in C major?
The answer is YES. Therefore this is a Major 2nd.
How can we turn this into a Minor 2nd? Bring it down a semitone!
A semitone lower than D is Db!
Remember this cannot be C sharp otherwise you actually change the intervals number!

What about this interval?
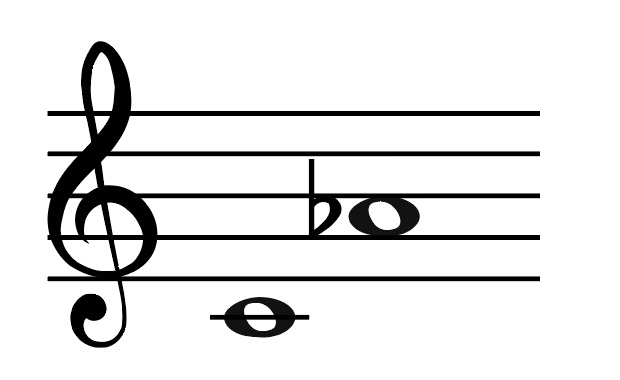
What is the intervals number?
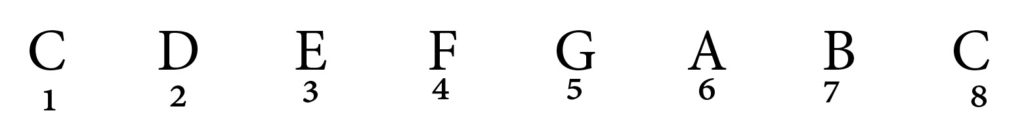
That’s correct, C-Ab is a 6th! Now, is Ab in C major? No it is not… we have an A natural in C major.

As you can see Ab is a semitone lower than A making this a MINOR 6th!
Last example…
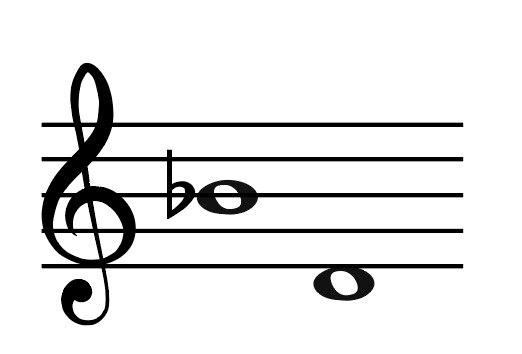
Now this interval we need to be really careful…
Remember that we must work out an interval from the LOWEST note… which is the lowest note?
That’s correct, it’s the D! So let’s write out the D major scale…
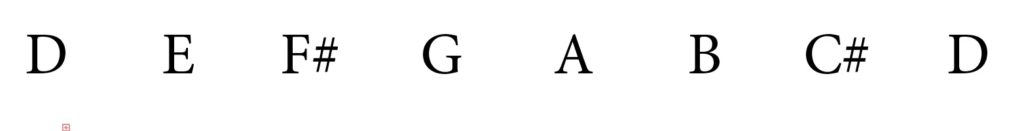
What is the interval between D and Bb? That’s correct it’s a 6th… but is Bb in D major? No it is not… we have a B natural in D major! Bb is a semitone smaller than B natural, making this a MINOR 6th!
A Final example
Let’s look at the below interval.

What is this intervals number (distance between the notes)?
Let’s write out the scale. Remember, we always work the interval out by going from bottom to top, so we need to write out the scale of G major…
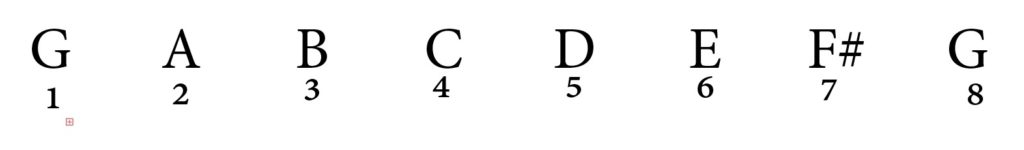
As you can see, B is the 3rd note of G major and this makes the interval a 3rd. In order to work out whether this is a major or minor interval we need to see if the top note is in the scale of the bottom note… so is B natural in G major?
The answer is YES! This makes the interval a MAJOR 3rd!
A minor 3rd is one semitone smaller than a major 3rd… let’s look at the piano

One semitone smaller than B is a Bb meaning that the below interval (G-Bb) is a minor 3rd!

Perfect intervals
These are the intervals of a 4th, 5th and 8ve! For these three intervals, we use the word perfect.
Remember ‘perfect’ is used because 4th, 5th and 8ve how a very stable consonant sound to them.
You can also remember them because the do not change in the major and minor scales.
Let’s compare G major and G minor scales…


As you can clearly see, the 4th, 5th and 8ve are all the same! (Just be sure to ignore the major 2nd interval which is present in the both the major and natural minor scales.
An example Perfect Intervals
Let’s have a look at the below interval.

Can you label this interval?
That’s correct, it is a PERFECT 5th. This is because C natural is the 5th note of the C major and C minor scales.
Ear Training and Intervals
To develop as a musician you’ll want to be able to recognise intervals by ear. This is where ear training comes in, as the more you practice, the better your’ll get.
My recommendation for this is Tonegym as they have a comprehensive and fun program for training your ears. It’s what has gotten the best results with for my own students.
In the ‘tools’ section of their site, Tonegym even have an interval memorizer that allows you to learn every type of interval.
For an in-depth look at ear training, here’s my full review of Tonegym.
Songs that use Major Intervals
Here are two example song that feature major intervals. I have chosen pieces in which the interval is prominent in the melody and so more memorable.
‘Symphony No. 5’ – Beethoven
Here the first two notes (G – Eb) are a descending Major 3rd. The third and fourth notes are a Minor 3rd (F – D). The major 3rd at the beginning is more unusual as the piece is in C minor. This is without doubt one of the most dramatic and famous examples of a Major 3rd in Western music.

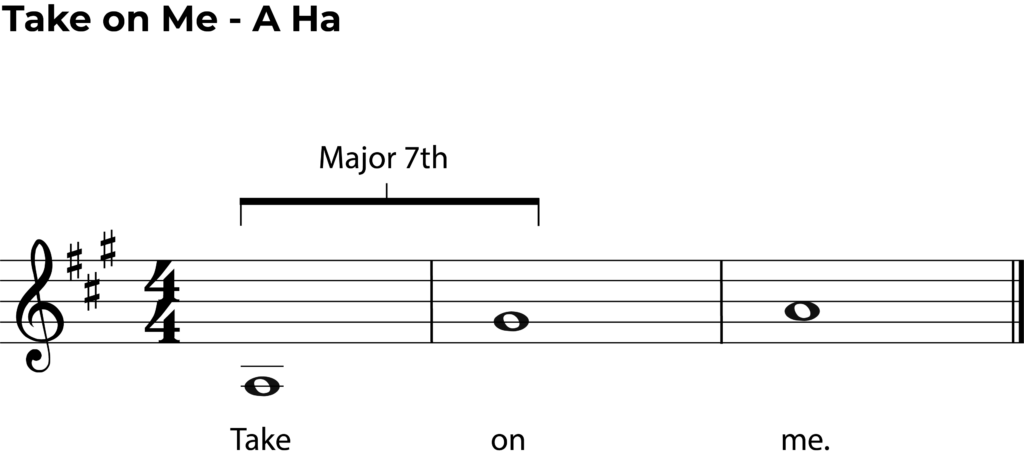
‘Take On Me’ – A Ha
“Take on Me” by A-ha is that super catchy ’80s song with the high-pitched singing you can’t help but hum along to. It’s got that synth-pop vibe and tells a story about going after love, making it a total banger that everyone knows and loves.
Songs that use Minor Intervals
Here are two examples of minor intervals in popular songs.
‘Jaws’ John Williams
Two bass notes, a minor 2nd, and such dread created with this famous sequence. The E natural to F natural is a Minor 2nd.

greensleeves
This traditional English folk song dates back to the 16th century. The E natural to G natural at the very beginning gives us a Minor 3rd interval.

Songs that use Perfect Intervals
There songs feature perfect intervals as part of the main melody or hook.
The Star Wars Theme
In the 2nd measure the G to D is a perfect 5th as D natural is the 5th note of the G Major scale.

‘Summer Nights’ – Grease
“Summer Nights” from Grease is like that catchy and fun tune that makes you want to dance and sing with your friends. It’s all about summer romance and gossip, with those memorable melodies and playful lyrics that’ll have you reminiscing about your own summer adventures.
The 2nd and 3rd notes of this famous riff give us the perfect 4th of D to G. G natural is the fourth note son the D major scale: D, E, F#, G.

What’s next…?
- Learn about two more interval types: augmented and diminished intervals
- Learn about intervals larger than an octave: compound intervals.
